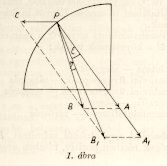
1. ábra
Eötvös Lorándnak egyes nevezetes tudományos alkotásait rövid jellemző elnevezéssel szokás megjelölni. Beszélünk a felületi feszültségre vonatkozó Eötvös-törvényről, a mozgó testek nehézségváltozását kifejező Eötvös-effektusról, és különösen újabban Eötvös-kísérlet néven említjük a tömegvonzás és a tehetetlenség arányosságára vonatkozó nagyjelentőségű vizsgálatait. Szakemberek előtt közismert, hogy Eötvös és munkatársai, Pekár Dezső és Fekete Jenő e vizsgálatokról készült munkájukkal 1909-ben a göttingeni egyetem Benecke-pályadíját nyerték el. A díjnyertes pályamunka anyagát Eötvös maga nem publikálta, néhány évvel halála után munkatársai mint posztumusz munkát tették közzé az Annalen der Physik 1922. évfolyamában. Ez a tanulmány némiképpen megrövidítve tartalmazza a pályamunkát. Valamivel teljesebben közölte az eredeti pályamunkát a Selényi Pál szerkesztésében Eötvös's Gesammelte Arbeiten címen 1953-ban megjelent gyűjtemény.
Eötvös azokat a vizsgálatokat, amelyeknek alapján a pályamunka elkészült, a századforduló első éveiben végezte munkatársaival együtt; azonban e kérdésre vonatkozó vizsgálatai korábbi időre nyúlnak vissza, úgyszólván egyidősek gravitációs kutatásaival. E tárgyú régebbi vizsgálatainak dokumentuma a Magyar Tudományos Akadémián 1889. január 20-án tartott beszámolója, amelynek anyaga magyar és német nyelven 1890-ben jelent meg.
A probléma régi keletű, mert tulajdonképpen azt a kérdést foglalja magában, hogy a nehézségi erőtérben változik-e a gyorsulás az anyagi minőséggel. Erre a kérdésre már Galilei klasszikus ejtési kísérletei adtak választ, majd később Newton lengésidő megfigyelései különböző fajta anyagokkal terhelt ingákon, amelyeket később mások, köztük Bessel nagyobb pontossággal megismételtek. Mindezek a kísérletek arra a megállapításra vezettek, hogy a tömegvonzás független az anyagi minőségtől.
Az évszázadokon át kiváló kutatók által végzett kísérletekben fokozatos fejlődés mutatkozott, amennyiben a mérések pontossága egyre inkább növekedett. Newton kísérleteinek pontossága 1/1000-ig terjedt, Besselnek a 19-ik század első felében különböző anyagú ingákkal végzett kísérletei 1/50 000 pontosságot értek el.
Eötvös a tömegvonzás és a tehetetlenség arányosságára vonatkozó s a múlt század 80-as éveiben végzett kísérleteiben az általa szerkesztett torziós ingát használta, s ugyanazt a módszert alkalmazta tökéletesített eljárással és nagyobb pontossággal századunk elején folytatott vizsgálataiban is. Az 1889-ben tartott akadémiai beszámoló szerint az akkor elért pontosság 1/20 000 000, míg a göttingeni pályamunkában közölt kísérleti vizsgálatok pontossága 1/200 000 000, vagyis 10-szer nagyobb. Eötvös a régebbi vizsgálatokban sárgaréz, üveg, antimonit és parafa esetében végzett kísérleteket. A göttingeni pályamunkához folytatott kísérletekben a megvizsgált anyagok a következők voltak: magnalium, kígyófa, vörösréz, víz, kristályos rézszulfát, rézszulfátoldat, azbeszt, faggyú, ezüstszulfát és vasszulfát. A felsorolt anyagokat Eötvös platinával hasonlította össze. Eötvösnek a tömegvonzás és a tehetetlenség arányosságára vonatkozó vizsgálatai az addigiaktól teljesen eltérő, eredeti elven alapulnak, s ezért méltán megilleti azokat az Eötvös-kísérlet elnevezés.
Eötvös vizsgálatainak az az elvi alapja, hogy
mivel a Föld forgásából származó
centrifugális erő mint tehetetlenségi erő
értelmezésénél fogva független
az anyagi minőségtől, ha a Földtől
származó tömegvonzás a különböző
minőségű anyagokra eltérő lenne,
akkor az eredő, vagyis a nehézségi erő
az anyagi minőség szerint változnék,
s a nehézségi erő iránya is a különböző
anyagokra más és más lenne. Ez más
szóval azt is jelenti, hogy minden anyagra nézve
más nívófelület alakulna ki. Az Eötvös-féle
torziós inga kiválóan alkalmas a nehézségi
erő irányában bekövetkező igen
kicsi eltérések megállapítására.

1. ábra
A következőkben röviden vázoljuk
Eötvös módszerét. Az 1. ábrán
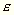 jelenti a vonzó erő és az eredő
nehézségi erő iránya közti szöget,
jelenti a vonzó erő és az eredő
nehézségi erő iránya közti szöget,
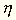 pedig az anyagi minőség különbözőségéből
származó feltételezett irányeltérést.
Az
pedig az anyagi minőség különbözőségéből
származó feltételezett irányeltérést.
Az 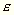 szög értéke a földrajzi szélességtől
függ, és legnagyobb értéke 45°
szélességen kb. 6'-et
tesz ki. Az ábra PBB1
szög értéke a földrajzi szélességtől
függ, és legnagyobb értéke 45°
szélességen kb. 6'-et
tesz ki. Az ábra PBB1
| háromszögéből | 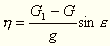 | , ahol G, illetve G1 az anyagi minőség szerint különböző gyorsulásokat |
| jelentik. |
| Feltételezzük, hogy G1 - G = KG, tehát | 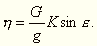 |
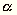 azimutszögű állásában:
azimutszögű állásában:
| (MblbKb-MalaKa) |
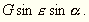 . . |
A torziós inga elméletéből
ismert egyensúlyi feltétel a horizontális
variométerre alkalmazva, figyelemmel az anyagi minőségtől
származó feltételezett különbségre
is:
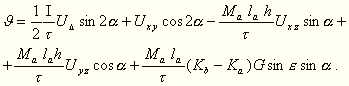
E képletben I a lengő rendszer
tehetetlenségi nyomatéka, 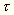 a szál csavarási
nyomatéka, h a mélyebben felfüggesztett
tömeg középpontjának távolsága
az ingarúd vízszintes síkjától.
a szál csavarási
nyomatéka, h a mélyebben felfüggesztett
tömeg középpontjának távolsága
az ingarúd vízszintes síkjától.
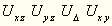 a nehézségi erőteret jellemző
második deriváltak.
a nehézségi erőteret jellemző
második deriváltak. 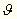 szög az eltérés
a meg nem csavart egyensúlyi helyzettől.
szög az eltérés
a meg nem csavart egyensúlyi helyzettől.
Eötvös e vizsgálataiban többféle eljárást alkalmazott. Az első eljárásnál feltételezte, hogy a nehézségi erőtér és a szál csavarási nyomatéka állandó. A másodiknál feltételezte az erőtér állandóságát, de a szál csavarási nyomatékára lassú változást engedett meg. A harmadik legpontosabb eljárásnál nem kellett sem az erőtér állandóságát, sem a torziós szál változatlanságát feltételezni.
Eötvös a harmadik eljárásnál kettős torziós ingát használt antiparallel ingarudakkal. A kísérletet úgy rendezte be, hogy az ingarúd felső tömegei ugyanolyan anyagból voltak Kb jellemző együtthatóval, a mélyebbre függesztett tömegek pedig az összehasonlításra kiválasztott különböző minőségű anyagok Ka, illetőleg K´a együtthatóval. A kettős ingát 90°-ként változó azimutállásokban észlelték.
Jelöljük a K-Ny állásokban nyert leolvasások
különbségét v-vel, az É-D
állások leolvasásainak különbségét
m-mel, s legyen 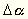 az a nagyon kicsi szög, amelyet a
kezdőállásban az ingarúd tengelye
a csillagászati északi iránnyal bezár.
az a nagyon kicsi szög, amelyet a
kezdőállásban az ingarúd tengelye
a csillagászati északi iránnyal bezár.
Két észlelési sorozatra van szükség:
az elsőnél az 1. ingarúdra a Ka
együtthatójú tömeg, a 2. ingarúdra
a K´a együtthatójú
tömeg van felfüggesztve. A megfelelő értékek
ekkor az 1. ingarúdra nézve v1
m1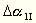 ,
a 2. ingarúdra nézve v´2
m´2
,
a 2. ingarúdra nézve v´2
m´2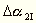 .
A második észlelési sorozatnál
a felfüggesztett tömegeket egymással felcseréljük,
s ekkor az 1. ingarúd adatai v´1
m´1
.
A második észlelési sorozatnál
a felfüggesztett tömegeket egymással felcseréljük,
s ekkor az 1. ingarúd adatai v´1
m´1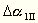 a 2. ingarúd adatai pedig v2 m
2
a 2. ingarúd adatai pedig v2 m
2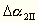 .
.
A v és m mennyiségek hányadosa
nem függ sem az érzékenység esetleges
megváltozásától, sem az erőtér
lassú változásától. A fentebb
említett egyensúlyi feltételből kiszámítható
az anyagi minőséget jellemző együtthatók
különbsége:
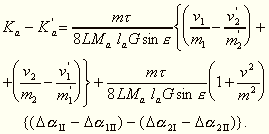
E képletben L a skálatávolság.
Eötvös e kísérleteivel kapcsolatban igen
gondosan megvizsgálta az elért pontosságot.
A fenti képletből látható, hogy ha
volna eltérés a különböző
minőségű anyagok tömegvonzásában,
akkor annak a 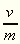 hányados értékében
kellene mutatkoznia. Mivel közvetlenül a v és
m mennyiségeket észlelték, ezek középértékének
középhibáiból a hibaterjedés
szabályai szerint a
hányados értékében
kellene mutatkoznia. Mivel közvetlenül a v és
m mennyiségeket észlelték, ezek középértékének
középhibáiból a hibaterjedés
szabályai szerint a 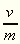 mennyiség középértékének
középhibája:
mennyiség középértékének
középhibája:
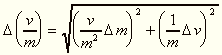 .
.
A 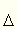 v és
v és
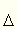 m
középhibákat Eötvös
a szokásos módon a
m
középhibákat Eötvös
a szokásos módon a 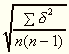 képlettel számította.
képlettel számította.
Egy-egy észlelési sorozat kb. 100 észlelésből
állott, s mivel egy-egy sorozaton belül a v és
m értékek alig változtak, a középértéktől
számított 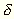 eltérések csekélyek
voltak, s ennek következtében a középértékek
eltérések csekélyek
voltak, s ennek következtében a középértékek
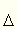 v és
v és
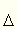 m
középhibái is igen kicsinyeknek adódtak.
Ez természetesen csak akkor várható, ha minden
olyan zavaró körülmény ki van küszöbölve,
amely az ingarúd egyensúlyi helyzetét megváltoztatni
képes. Eötvös különösen nagy gondot
fordított e zavarok kiküszöbölésére.
A torziós ingában gondosan preparált
és ellenőrzött szálakat használt.
Megszüntette az esetleges elektrosztatikai és mágneses
hatásokat, és olyan hőmérsékleti
védelmet biztosított a műszernek, hogy hőmérsékletváltozásból
származó zavaró hatások nem léptek
fel. A felsorolt zavaró hatások v és m
értékeiben jelentkezhetnek, s ha nincsenek kellően
kiküszöbölve, akkor elfedhetik azt a hatást,
amelyet az anyagi minőség különbözősége
a tömegvonzásban esetleg előidézhet.
Az Eötvös kísérleteiben elért pontosság
nagyságrendjét a következő adatok jellemzik.
A kb. 100-as észlelési sorozatokban a v és
m mennyiségek középértékeinek
középhibái általában ±0,01 skálaosztás
rendűek. A hibaterjedés szabályai szerint
a
m
középhibái is igen kicsinyeknek adódtak.
Ez természetesen csak akkor várható, ha minden
olyan zavaró körülmény ki van küszöbölve,
amely az ingarúd egyensúlyi helyzetét megváltoztatni
képes. Eötvös különösen nagy gondot
fordított e zavarok kiküszöbölésére.
A torziós ingában gondosan preparált
és ellenőrzött szálakat használt.
Megszüntette az esetleges elektrosztatikai és mágneses
hatásokat, és olyan hőmérsékleti
védelmet biztosított a műszernek, hogy hőmérsékletváltozásból
származó zavaró hatások nem léptek
fel. A felsorolt zavaró hatások v és m
értékeiben jelentkezhetnek, s ha nincsenek kellően
kiküszöbölve, akkor elfedhetik azt a hatást,
amelyet az anyagi minőség különbözősége
a tömegvonzásban esetleg előidézhet.
Az Eötvös kísérleteiben elért pontosság
nagyságrendjét a következő adatok jellemzik.
A kb. 100-as észlelési sorozatokban a v és
m mennyiségek középértékeinek
középhibái általában ±0,01 skálaosztás
rendűek. A hibaterjedés szabályai szerint
a 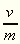 mennyiségek
középhibái kb. ±0,002 rendűek; a
mennyiségek
középhibái kb. ±0,002 rendűek; a
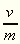 hányadosok különbségei összegének
középhibája kb. ±0,004. Ha ezt megszorozzuk
a kb. 0,4 · 10-6 értékű
külső tényezővel, a középhiba
kb. 0,0016 · 10-6 értékű.
Vegyük figyelembe, hogy Eötvös több kísérleti
sorozatában a vizsgált anyag valamilyen tartályban,
fém- vagy üvegcsőben volt elhelyezve, s ezért
a hibát csupán a vizsgált anyagból
álló tömegrészre kell vonatkoztatni.
Emiatt a középhiba megnövekedik kb. ±0,003 · 10-6
értékre. A Ka-K´a
különbségek az észlelésekből
0,001 · 10-6-0,006 · 10-6
értékűeknek adódtak, tehát a
számított középhibáknál
részben kisebbek, részben nagyobbak, nagyságrendjük
azonban végeredményben a középhibák
nagyságrendjével volt megegyező.
hányadosok különbségei összegének
középhibája kb. ±0,004. Ha ezt megszorozzuk
a kb. 0,4 · 10-6 értékű
külső tényezővel, a középhiba
kb. 0,0016 · 10-6 értékű.
Vegyük figyelembe, hogy Eötvös több kísérleti
sorozatában a vizsgált anyag valamilyen tartályban,
fém- vagy üvegcsőben volt elhelyezve, s ezért
a hibát csupán a vizsgált anyagból
álló tömegrészre kell vonatkoztatni.
Emiatt a középhiba megnövekedik kb. ±0,003 · 10-6
értékre. A Ka-K´a
különbségek az észlelésekből
0,001 · 10-6-0,006 · 10-6
értékűeknek adódtak, tehát a
számított középhibáknál
részben kisebbek, részben nagyobbak, nagyságrendjük
azonban végeredményben a középhibák
nagyságrendjével volt megegyező.
Eötvös ezekből az eredményekből arra a megállapításra jutott, hogy ha lenne eltérés a különböző anyagok vonzásában, akkor annak 0,005 · 10-6 értéknél kisebbnek kellene lennie. Ilyen módon az Eötvös kísérleteiben elért pontosság 1/200 000 000.
Eötvös a fentebb felsorolt anyagok vizsgálatán kívül különleges kísérleteket végzett radioaktív anyagokkal. Az a kor, amelyben Eötvös a tömegvonzás és a tehetetlenség arányosságára vonatkozó igen pontos kísérleteit elvégezte, a radioaktív jelenségek felfedezésének időszaka volt. R. Geigelnek volt akkor olyan elképzelése, hogy a radioaktív sugárzás a vonzási energiát elnyeli. Eötvös kis üvegcsőbe szórt rádiumpreparátumot helyezett el a torziós ingarúdon levő platinatömeg közelébe, és az üvegcső helyzetétől függően kis taszító, illetőleg vonzó hatást tapasztalt. A kísérletet úgy ismételte meg, hogy a rádiumpreparátumot tartalmazó üvegcső helyébe olyan üvegcsövet helyezett el, amelyben áramkörbe kapcsolt vékony platinaszál volt beforrasztva. Amikor áram bevezetésével a platinaszál annyi hőt termelt, amennyit a rádiumpreparátum sugárzása kiadott, akkor a taszító, illetőleg a vonzó hatás ugyanakkorának adódott, tehát a jelenség a hőhatással teljesen meg volt magyarázva. A tömegvonzás abszorpciójának nyoma sem volt.
Az 1930-1935. években Eötvös vizsgálatai nyomán magam is foglalkoztam a tömegvonzás és a tehetetlenség arányosságának kérdésével. Az volt a törekvésem, hogy a pontosságot tovább fokozzam, és a vizsgálatokat Eötvös kísérleteiben nem szereplő egyéb anyagokra is kiterjesszem.
A kísérletek céljára a Geofizikai Intézet III. jelzésű kettős torziós ingáját használtam, amely abban az időben a legmegbízhatóbb laboratóriumi műszernek bizonyult. Különösen azzal tűnt ki, hogy úgyszólván teljesen érzéketlen volt a hőmérsékleti hatásokkal szemben. A torziós szálak régen preparált platina-iridium szálak voltak, amelyeknek hőmérsékleti együtthatója gyakorlatilag zérus volt, és nem volt semmiféle rugalmas járásuk. Külön gondoskodás történt az állandó hőmérsékletű környezetről. A földmágneses teret Eötvöshöz hasonlóan kompenzáltam, és ezenkívül magukat az észleléseket is felhasználtam az esetleges mágneses hatás megállapítására. Ezt azzal értem el, hogy az É-D és K-Ny főirányokon kívül ezekkel 45°-ot bezáró közbeiktatott állásokban is végeztem észleléseket. Ez utóbbiakból az esetleges mágneses hatás kiszámítható és javításba vehető. Ezt az eljárást a sárgaréznek és a diamágneses bizmutnak összehasonlításánál alkalmaztam. Egyébként a 45°-os közbeiktatott állásokban végzett megfigyelések magukban is olyan sorozatot alkotnak, amelyből a Ka-K'a különbségek a főállásokban végzett észlelések eredményétől függetlenül is meghatározhatók s így ellenőrzésül szolgálhatnak. Ezt a vizsgálatot vörösréz és mangánrézöntvény összehasonlításánál végeztem el, és a kétféle észlelési sorozatból egymástól függetlenül a következő eredményeket kaptam:
a főállásokban: Ka-K´a
= + 0,08 · 10-9 ± 0,20 · 10-9
a közbeiktatott állásokban:
Ka-Ka = + 0,12 · 10-9 ± 0,22 · 10-9
Az anyagi minőséget jellemző együtthatók különbségei mindkét sorozatban a hibahatáron belül voltak, s a középértékek középhibája kb. ± 0,2 · 10-9, vagyis 1/5 000 000 000, ami az Eötvös-féle kísérletek pontosságát 25-szörösen múlja felül.
A többi kísérletnél a középhibák rendje kb. ± 0,5 · 10-9, vagyis 1/2 000 000 000, tehát a pontosság általában 10-szerese Eötvös kísérletei pontosságának.
Az összehasonlított anyagok a már említetteken kívül a következők voltak:
platina - sárgaréz
batáviai üvegcseppek - sárgaréz
batáviai üvegtörmelék - sárgaréz
paraffin - sárgaréz
alumíniumfluorid - vörösréz
Az észlelési sorozatokból számított Ka-K´a különbségek részben pozitív, részben negatív előjelűek voltak, a középhibák ugyanolyan rendűek, és azok középértéke ± 0,52 · 10-9.
Eötvös még egy másik módszert is alkalmazott a tömegvonzás és a tehetetlenség arányosságának megvizsgálására. Ez a módszer a Naptól származó árapálykeltő erőnek és a Föld keringési pályáján fellépő centrifugális erőnek összehasonlításán alapul. Ennek a jelenségnek a megvizsgálására is igen alkalmas a torziós inga. Tegyük fel, hogy a meridiánba beállított ingarúd végein különböző minőségű tömegek vannak, és pl. az északi végen levő tömegre a Nap vonzása nagyobb lenne, mint a délen levő tömegre. Ekkor napkeltekor az északon levő tömeg a Nap felé, vagyis kelet felé mozdulna el, s az ingarúd annak megfelelően fordulna el; napnyugtakor viszont az északon levő tömeg nyugat felé mozdulna el, s az ingarúd az előbbihez képest ellenkező irányban fordulna el. Az ingarúd tehát a fajlagos tömegvonzás következtében 24 órás periódusú lengő mozgást végezne, amelyet megfelelő érzékenységű ingával meg is lehetne figyelni. Ennek a módszernek az előbbiekben tárgyalttal szemben az az előnye van, hogy a torziós inga az egész észlelési sorozat folyamán ugyanabban az azimutállásban marad, és a megfigyelés tárgya az egyensúlyi helyzet esetleges megváltozása kell legyen. Viszont a módszer érzékenysége kb. harmadrésze az előbbi módszer érzékenységének.
Eötvös és munkatársai ezzel a módszerrel magnálium és platina vonzási együtthatóját hasonlították össze, s a Ka-K´a különbség ugyanakkora rendűnek adódott, mint a másik módszerrel végzett kísérletekben. Ilyen kísérletek céljára különösen alkalmas Eötvösnek igen érzékeny műszere, a gravitációs kompenzátor.
A legutóbbi években a tömegvonzás és a tehetetlenség arányosságának megvizsgálására lényegében ugyanezt az elvet használta fel R. H. Dicke amerikai kutató, azonban kísérleteiben korszerű technikával kidolgozott műszert használt.
Dicke három szálon háromszög alakú keretet függesztett fel, s a háromszög csúcsait egyenlő tömegekkel terhelte meg. Ezek közül kettő vörösréz, a harmadik pedig hengeres tubusba öntött ólomklorid volt. A háromszög alakú keret egyik beezüstözött oldaláról visszavert fény megfelelő optikai berendezéssel egy, másodpercenként 3000 rezgést végző drótszálra esik, onnan egy fotocellára jut, amelynek állandó megvilágítás mellett meghatározott áramerőssége van, tehát a háromszögű keret változatlan állásának állandó áramerősség felel meg. Ha a háromszögű keret csak kicsit is elfordul, a fotocellából érkező jel módosul és olyan egyenfeszültséget létesít, amely egy szervomechanizmus segítségével az egyik vörösréztömeget s vele együtt az egész rendszert eredeti helyzetébe viszi vissza. A visszaállító erőt regisztrálják, s ez a mértéke a felfüggesztett rendszer elfordulásának. Dicke az egész rendszert jól záró fémedénybe helyezte, és abból a levegőt 10-6 higanymm-nyi nyomásig kiszivattyúzta. Ezáltal a légáramlások zavaró hatását teljesen megszüntette. Az egész berendezést 4 m mélyen levő kamrában szerelte fel. Közlése szerint sok műszaki nehézség leküzdése után az eredeti Eötvös-féle kísérletek pontosságát 50-szeresre, s a 30-as években végzett kísérleteim pontosságát 5-szörösre sikerült fokoznia. Legújabb értesülések szerint a pontosság Dicke kísérleteiben még tovább növekedett 10-11 nagyságrendig.
A következőkben röviden rámutatni kívánok az Eötvös-kísérlet jelentőségére egyrészt az általános relativitás-elmélet, másrészt a modern atomfizika szemszögéből.
Ismeretes, hogy Einstein általános relativitási elméletének alapja az ekvivalencia elve, amelynek értelmében a vonzó és a tehetetlen tömeg azonos. Valószínű, hogy amikor Einstein elméletét megalkotta, még nem ismerte Eötvös kísérleteinek eredményeit, s azokkal csak később ismerkedett meg. Einstein mindenképpen, a kísérleti eredményektől függetlenül meg volt győződve az ekvivalencia elvének helyességéről. Törekvése az volt, hogy a mozgási törvényeket gyorsuló rendszerekre állapítsa meg. Ezért kellett az inerciaerőket a gravitációs erőkkel azonosítania, ami azt jelenti, hogy egy gyorsuló rendszerben a külvilágtól elzárt megfigyelő nem tudja megkülönböztetni azt, hogy valamely tömeg mozgását a gravitációs tér vagy pedig a tehetetlenség hozza létre.
Az Eötvös-kísérletnek újabban az atomfizikában is van jelentősége. Ugyanis a jelenleg ismert sokféle elemi részecske között vannak olyanok, amelyek csupán elektromos töltésük előjelében különböznek egymástól. Ilyenek az elektron és pozitron, a proton és antiproton stb. Vannak ún. antirészecskék, amelyek többnyire a hatalmas gyorsító berendezésekben jelennek meg és igen rövid élettartamúak. Bondi angol fizikus azt a hipotézist állította fel, hogy az antirészecskék gravitációs hatása taszító volna. E hipotézis szerint a részecskék és az antirészecskék között nem volna érvényes a tömegvonzás és a tehetetlenség arányossága, tehát az antirészecskéket tartalmazó anyagra nem volna érvényes az ekvivalencia elve. Mivel az antirészecskék a mi világunkban ritkán jelennek meg, úgy látszik, hogy az ekvivalencia elvet ilyen vonatkozásban kísérletileg megvizsgálni nem lehet. L. J. Schiff kaliforniai kutató rámutatott arra, hogy a mi világunk atomjaiban is találhatók antirészecskék, mert az atom belsejében levő elektromos terek virtuális elektron-pozitron párokat hoznak létre, s ha a pozitronok gravitációja ellentett előjelű volna, mint az elektronoké, annak a tömegvonzás és a tehetetlenség arányosságára vonatkozó nagy pontosságú kísérletekben mutatkoznia kellene. Márpedig az eddig elért nagy pontosság mellett ilyen jelenségnek semmi nyoma sincsen, tehát nincs antigravitáció. Mindenesetre ez a probléma hozzájárult ahhoz, hogy a tömegvonzás és a tehetetlenség arányosságára vonatkozó kísérletek ismét az érdeklődés előterébe kerültek, és a mai kutatók a pontosságnak még további fokozására törekednek.
Igen érdekesek Eötvösnek a tömegvonzás
abszorpciójára vonatkozó vizsgálatai,
amelyekről szintén a göttingeni pályamunkában
számolt be. Eötvös e vizsgálatok céljára
az általa szerkesztett gravitációs kompenzátort
használta. Ez igen érzékeny műszer,
és érzékenysége az ingarúd
végei közelében felszerelt kvadráns
alakú ólomtömegek megfelelő beállításával
úgyszólván minden határon túl
fokozható. Ha az ólomkvadránspárok
középvonalai a függőlegeshez viszonyítva
45°-ra illetőleg 225°-ra vannak beállítva,
akkor az egyik kvadráns a vízszintes sík
alá, a másik pedig föléje esik; a kvadránspárok
középvonalának 135°-os és 315°-os
beállításakor pedig azok a kvadránsok
kerülnek a vízszintes sík fölé,
amelyek előbb alatta voltak és viszont. Mindegyik
esetben a Föld egyik felének vonzása úgy
érvényesül, hogy közben van a kvadráns
ólomtömege, a Föld másik felének
vonzását pedig nem árnyékolja az ólomtömeg.
Ha lenne a tömegvonzásnak abszorpciója, akkor
a tömegvonzásnak azon az oldalon kellene nagyobbnak
lennie, amelynél nincsen árnyékoló
tömeg. (2. ábra.)
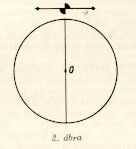
2. ábra.
Ha a kvadránsok egyes állásaiban a torziós ingán nyert leolvasásokat rendre n1 n2 n3 n4betűkkel jelöljük, akkor Eötvös számításai szerint az abszorpciós együttható kifejezése:
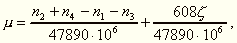
ahol 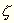 jelenti a torziós ingarúd végén
levő tömeg súlypontjának függőleges
koordinátáját olyan koordináta-rendszerben,
amelynek kezdőpontja a szemben levő kvadránsok
középpontján átmenő vízszintes
vonalon van. Ha az ingarúd a kvadránsokhoz viszonyítva
centrikusan van elhelyezve, amire törekedni kell a beállításkor,
akkor a fenti kifejezésben a
jelenti a torziós ingarúd végén
levő tömeg súlypontjának függőleges
koordinátáját olyan koordináta-rendszerben,
amelynek kezdőpontja a szemben levő kvadránsok
középpontján átmenő vízszintes
vonalon van. Ha az ingarúd a kvadránsokhoz viszonyítva
centrikusan van elhelyezve, amire törekedni kell a beállításkor,
akkor a fenti kifejezésben a 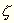 -t tartalmazó
tag elhanyagolható.
-t tartalmazó
tag elhanyagolható.
Az elvégzett kísérletek eredményei szerint az első tag számlálója egységnyi nagyságrendű, s így megállapítható, hogy ha a tömegvonzásnak lenne abszorpciója, akkor a kompenzátor ólomkvadránsainak abszorpciója egy ötvenmilliárdodnál kisebb kell legyen. Ez az árnyékolás megfelel kb. 5 cm vastag ólomrétegnek. 1 méter vastag ólomrétegre átszámítva az elnyelés kisebb lenne egy kettőezerötszázmilliomodnál. Ezen az alapon számítva az egész Földnek az abszorpciója az átmérője mentén legfeljebb egy nyolcszázad volna.
Ha az abszorpciót az árapályjelenségre
alkalmazzuk, akkor a Naptól származó hatásnál
a 0 és 180° zenitállások összehasonlításakor
a szoláris hatás a következőképpen
fejezhető ki:
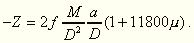
E kifejezésben a a Föld sugara, D a Nap távolsága, M a Nap tömege. Ha µ helyébe a kompenzátorral végzett kísérletek eredményeit felhasználva 1/1600-at teszünk, akkor a Naptól származó árapálykeltő erőhatás:
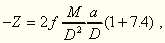
tehát az abszorpció az árapálykeltő erőt kb. 8-szorosára növelné, ami teljesen ellentmond a tapasztalatnak. Eszerint a fentebb említett abszorpció sem lehetséges.
Eötvös Lorándnak, nagy természettudósunknak a gravitáció körében kifejtett tudományos munkássága igen széles körű, elért eredményei pedig alapvető jelentőségűek. Azok a problémák, amelyekkel oly behatóan és nagy sikerrel foglalkozott, most is, félévszázad múltán is korszerűek, a jelenkor kutatóiban gondolatokat ébresztenek, s további kutatásokra ösztönöznek.
Renner János
Eötvös Loránd Geofizikai Intézet
Budapest