Vor ungefähr zehn Jahren habe ich eine Methode zur Beobachtung der Kapillaritätskonstanten ersonnen, welche es ermöglichte, die Gestalt der Oberfläche ruhender Flüssigkeiten in ihrer ganzen Ausdehnung zu untersuchen, und die mir deshalb zur Prüfung der Resultate der Kapillaritätstheorie als besonders geeignet schien. Letzteres war auch das Ziel, welchem ich ursprünglich zustrebte; doch erweiterte sich bald das Feld meiner Untersuchungen: die Erscheinungen der Elektrokapillarität, die Frage nach der sogenannten Wirkungssphäre drängten sich mir unwillkürlich auf und fanden teilweise auch ihre Lösung.
Unterdessen gelang es mir, die Oberflächenspannung der Flüssigkeiten auf beliebig lange Zeit unverändert zu erhalten, sodaß ich ihre wahren Werte mit Sicherheit bestimmen konnte. Nach Beseitigung dieses hauptsächlichen Hindernisses konnte ich mich, besonders angeregt durch die Untersuchungen des Hrn. van der Waals an die wichtigste Frage dieses Gebietes heranwagen, nämlich den Zusammenhang der Oberflächenspannung mit der chemischen Zusammensetzung der Flüssigkeiten zu suchen.
Die hauptsächlichsten Resultate meiner bisherigen Untersuchungen
habe ich wohl von Zeit zu Zeit der ungarischen Akademie der Wissenschaften
in Form kurzer Mitteilungen vorgelegt, doch zögerte
ich mit ihrer ausführlichen Veröffentlichung, da sich
mir mit jedem neuen Resultate auch neue Aufgaben stellten, deren
Lösung mir ebenfalls wünschenswert schien. Doch das
rege Interesse für alle Fragen bezüglich des Zusammenhanges
der physikalischen und chemischen Eigenschaften der Körper,
welches in neuerer Zeit eine Reihe sorgfältiger Arbeiten
hervorrief, veranlaßt mich, die Resultate jenes Teiles meiner
Untersuchungen, welcher sich auf diese Frage bezieht, im Auszuge
zu veröffentlichen. Eine vollständigere Ausarbeitung
meiner Untersuchungen soll später folgen.
Zur Bestimmung der Kapillaritätskonstante bediene ich mich
seit dem Jahre 1876 einer Methode, welche ich die Reflexionsmethode
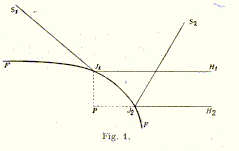
nennen will. Im wesentlichen besteht diese in Folgendem. Auf die
Oberfläche FF der Flüssigkeit fallen zwei von den Lichtquellen
S1 und S2 ausgehende Strahlenbündel
S1J1 und S2J2,
welche, an derselben reflektiert, in das horizontal gestellte
Fernrohr eines Kathetometers gelangen. Im Gesichtsfelde des Fernrohres
erscheinen dann zwei horizontale Lichtstreifen, welche die Lage
jener Teile der Oberfläche kennzeichnen, welche die von dem
einen, resp. dem anderen einfallenden Lichtbündel herrührenden
Strahlen in horizontaler Richtung reflektieren. Die Neigung der
Oberfläche in den Punkten J1 und J2
läßt sich aus der Richtung der einfallenden Strahlen
mit Hilfe des Reflexionsgesetzes bestimmen.

Die vertikale Entfernung J1P dieser Punkte wird mit dem Kathetometer gemessen. Mit Hilfe dieser durch die Beobachtung bestimmten Größen läßt sich die Kapillaritätskonstante aus den für die betreffende Oberfläche durch die Theorie gegebenen Gleichungen berechnen.
Zur Erklärung möge das Beispiel der kapillaren Zylinderfläche dienen, welches von einer Flüssigkeit längs der ebenen Seitenfläche eines größeren Gefässes gebildet wird. Die Theorie gibt für dieselbe folgende Gleichung:
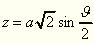
wo a die Quadratwurzel aus der Kapillaritätskonstante,
z die von der Niveauebene abwärts gerichtete vertikale
Ordinate und  den Winkel bedeutet, welchen
die Normale der Oberfläche mit der Vertikalen bildet. Bezeichnen
wir nun mit
den Winkel bedeutet, welchen
die Normale der Oberfläche mit der Vertikalen bildet. Bezeichnen
wir nun mit 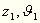 und
und 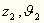 diese Größen für zwei Punkte der Fläche,
so erhalten wir für die Größe a die Gleichung:
diese Größen für zwei Punkte der Fläche,
so erhalten wir für die Größe a die Gleichung:
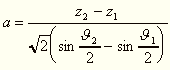
worin z2 - z1,sowie auch
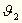 und
und 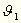 durch Messung bestimmt werden.
durch Messung bestimmt werden.
Diese hier in kurzen Umrissen angedeutete Methode habe ich sowohl an kapillaren Zylinderflächen, als auch an Rotationsflächen verwertet. Je nach den Umständen wählte ich die Richtung der einfallenden Strahlen so, daß sie außerhalb oder innerhalb der Flüssigkeit zur Oberfläche gelangten. Im Falle von Rotationsflächen, wie sie in Röhren mit verhältnismäßig kleinen Durchmessern (etwa 5 bis 20 mm) entstehen, wo uns keine von der Theorie gegebenen Formeln zu Gebote stehen, bestimmte ich die Größe a durch vergleichende Messungen mit Hilfe von Flüssigkeiten, deren Kapillaritätskonstanten mir schon bekannt waren.
Ich habe diese Methode bei einigen speziellen Untersuchungen auch
noch in der Weise abgeändert, daß ich statt des Kathetometers
ein horizontal verschiebbares, vertikales Fernrohr benutzte und
damit die horizontale Entfernung zweier Punkte messend, diese
zur Berechnung der Konstante a verwertete.
Die Vorteile dieser Methode bestehen in Folgendem:
1. Sie ist unabhängig von jeder Annahme bezüglich des Berührungswinkels, sowie auch von der Art der Benetzung der festen Gefäßwände.
2. Ich konnte mit Hilfe derselben Messungen auch an Flüssigkeiten vornehmen, welche in zugeschmolzenen Glasgefäßen enthalten, nur mit ihren eigenen Dämpfen in Berührung standen. Hierdurch erreichte ich eine kaum geahnte Konstanz der Oberflächenspannung, womit das größte Hindernis bei Beobachtung kapillarer Erscheinungen behoben wurde. Messungen an der Oberfläche des Wassers in diesen Gefäßen ergaben bei derselben Temperatur auch nach Jahren denselben Wert der Kapillaritätskonstante.
3. Diese Methode ermöglichte, die Veränderung der Kapillaritätskonstante auch bei Temperaturen zu verfolgen, welche weit über der Siedetemperatur der Flüssigkeit lagen, so z. B. bei Alkohol bis zu 236° C, bei Aethyläther bis zu 190° C. Auch war es möglich, die Kapillaritätskonstante kondensierter Gase, wie jene der Kohlensäure, der Schwefelsäure u. a. zu bestimmen.
4. Die Vergleichung der auf diese Weise gewonnenen Resultate mit
den aus Beobachtungen der Steighöhe in kapillaren Röhren
gewonnenen ergeben auch einen Aufschluß über die Größe
des Kontingenzwinkels.
Vergleiche zwischen den physikalischen und chemischen Eigenschaften verschiedener Körper können nicht, wie dies bisher in den meisten Fällen geschah, bei derselben, und zwar willkürlich gewählten Temperatur oder Druck, sondern nur bei solchen verschiedenen Temperaturen gemacht werden, welche für jeden der zu vergleichenden Körper einzeln durch die auf denselben Bezug habenden Größen bestimmbar sind.
Auf welche Weise dies geschehen kann, zeigte van der Waals, indem er die Körper in übereinstimmenden Zuständen, d. h. bei solchen absoluten Temperaturen verglich, welche gleiche Teile ihrer absoluten kritischen Temperaturen waren. Allein die kritischen Temperaturen bieten einen sehr unsicheren Ausgangspunkt für ähnliche Untersuchungen nicht nur wegen der Schwierigkeit ihrer Bestimmung, sondern auch weil die Möglichkeit einer chemischen Dissoziation bei diesen hohen Temperaturen nicht mit Sicherheit ausgeschlossen werden kann, ja sogar in manchen Fällen mehr als wahrscheinlich ist.
Um diesen Schwierigkeiten auszuweichen, ging ich von einer anders
formulierten Definition der übereinstimmenden Zustände
aus. Betrachten wir nämlich einen teilweise in flüssigem
und teilweise in gesättigtem Dampfzustande befindlichen chemisch
homogenen Körper als ein System von Molekülen gleicher
Masse, so läßt sich der Zustand desselben durch die
Art der Verteilung seiner Moleküle im Raume bestimmen. Bezeichnet
nun v das Molekularvolumen der Flüssigkeit, also den
Mittelvert des Raumes, den ein Molekül in der Flüssigkeit
einnimmt, und u dasselbe des gesättigten Dampfes,
so kann das Verhältniß v/u zur Bestimmung des
Zustandes dienen. Wenn nun dieses Verhältnis für zwei
chemisch verschiedene Körper bei entsprechenden Temperaturen
T1 und T2 denselben Wert hat,
so sind sie auf ähnliche Weise aus ihren Molekülen
zusammengesetzt. In solchen Zuständen ähnlicher Zusammensetzung
besteht dann für die beiden Körper die Gleichung:
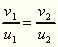
welche infolge der auf das Gasvolumen bezüglichen Sätze
die Form:
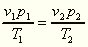
annimmt, worin p1 und p2 die Spannkräfte des gesättigten Dampfes der beiden Körper bei ihren absoluten Temperaturen T1 und T2 bedeuten. Aus diesen Gleichungen ist ersichtlich, daß die beiden Körper dann auch im Sinne der van der Waals'schen Festsetzung in übereinstimmenden Zuständen sich befinden.
Ich versuchte nun, Folgerungen aus der Annahme zu ziehen, daß Körper, welche sich im entsprechenden Zustande, also im Zustande ähnlicher Zusammensetzung befinden, auch im mechanischen Sinne ähnlich seien, nämlich bezüglich der zwischen ihren entsprechenden Teilen wirkenden Kräfte und deren Energien.
Betrachten wir nämlich einen Teil der Oberfläche einer
Flüssigkeit, welcher durch n Moleküle bedeckt
wird, so ist die auf denselben vom Dampfe ausgeübte Druckkraft:
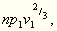
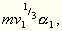
 die Oberflächenspannung, d.
h. die auf die Einheit bezogene Oberflächenenergie bezeichnet.
die Oberflächenspannung, d.
h. die auf die Einheit bezogene Oberflächenenergie bezeichnet.
Bilden wir nun diese Größen für die entsprechenden,
also aus derselben Anzahl der Moleküle gebildeten Teile eines
zweiten Körpers, so erhalten wir für dieselben:
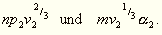
Aus obiger Annahme folgt dann für übereinstimmende Zustände
:
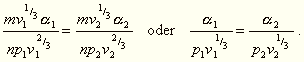
Durch ähnliche Betrachtungen bezüglich der Energien
einander entsprechender Teile ergibt sich für übereinstimmende
Zustände die Beziehung:
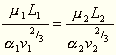
worin 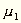 und
und 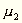 die
Molekulargewichte, L1 und L2
die latenten Dampfwärmen bezeichnen.
die
Molekulargewichte, L1 und L2
die latenten Dampfwärmen bezeichnen.
Bei der Ableitung dieser Sätze habe ich vorausgesetzt, daß
die Moleküle der Flüssigkeit mit denen des Dampfes gleiche
Massen haben. Flüssigkeiten, für welche dies zutrifft,
will ich schlechtin einfach zusammengesetzte nennen. Durch Einführung,
dieser Benennung können die oben gewonnenen Sätze
auf folgende Weise zusammengefasst werden: Besteht für irgend
zwei einfach zusammengesetzte Flüssigkeiten bei ihren absoluten
Temperaturen T1 und T2 die
Gleichung:

so bestehen für dieselben Temperaturen auch die folgenden:

Ferner erhalten wir durch Verbindung der Gleichungen (1) und (2)
auch noch:
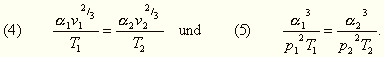
Die Gl. (3) enthält einen von Waterston schon im Jahre 1858, aber in unvollkommener Weise, nämlich für beliebige Temperaturen ausgesprochenen Satz. Auch van der Waals stellte zwei hierauf bezügliche Sätze auf, von denen der eine sich nur dadurch von dem durch die Gl. (5) ausgesprochenen unterscheidet, daß darin Druck und Temperatur auf den kritischen Zustand bezogen sind. Dieser letztere Umstand erklärt es auch, warum ihm die Bestätigung nicht gelingen konnte.
Aus den oben abgeleiteten Beziehungen, namentlich jener in Gl. (4) enthaltenen, habe ich noch weitere Folgerungen gezogen, welche den engen und einfachen Zusammenhang des Molekularvolumens mit der Oberflächenspannung noch deutlicher zeigen.
Infolge der Betrachtungen des Hrn. van der Waals gelangen
zwei Körper, welche bei den absoluten Temperaturen T1
und T2 in übereinstimmenden Zuständen
sind, wieder in solche, wenn die Zuwächse ihrer Temperaturen
mit T1 und T2 proportional
sind. Für übereinstimmende Zustände folgt daher
aus der Gl. (4):
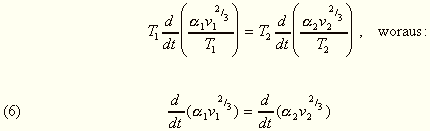
folgt. Ich habe den Wert dieses Quotienten für Aethyläther in Temperaturintervallen von 0 bis 190° C sorgfältig bestimmt und konnte keine Veränderlichkeit desselben mit der Temperatur nachweisen. Ist aber dies für einen Körper der Fall, so muß dasselbe infolge der Gl. (6) auch für alle anderen einfach zusammengesetzten Körper in entsprechenden Temperaturintervallen gelten. Untersuchungen an diesen Körpern zeigten auch die Konstanz dieses Quotienten innerhalb noch weiterer Temperaturgrenzen.
So gelangte ich zu dem folgenden Satze: Der
Quotient 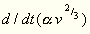 hat für alle einfach zusammengesetzten Flüssigkeiten
denselben von der Temperatur unabhängigen Wert, wenigstens
bei Temperaturen, welche höher sind, als die in der Mitte
zwischen dem absoluten Nullpunkt und der absoluten kritischen
Temperatur gelegene.
hat für alle einfach zusammengesetzten Flüssigkeiten
denselben von der Temperatur unabhängigen Wert, wenigstens
bei Temperaturen, welche höher sind, als die in der Mitte
zwischen dem absoluten Nullpunkt und der absoluten kritischen
Temperatur gelegene.
Selbstverständlich ist damit eine Konstanz nur insofern gemeint,
als sich dieselbe durch die Genauigkeit meiner bisherigen Beobachtungen
nachweisen läßt; dabei ist es nicht ausgeschlossen,
daß noch genauere Versuche, namentlich innerhalb weiterer
Temperaturgrenzen, eine Abhängigkeit dieser Größe
von der Temperatur zeigen würden. Den Wert dieser Konstante
fand ich - wie nachstehend ausführlich gezeigt werden soll,
gleich 0,227, wobei das Molekularvolumen v durch das Verhältnis
des Molekulargewichtes zu der Dichte berechnet wurde, ferner als
Einheit der Oberflächenspannung in üblicher Weise jene
diente, welche in der Oberfläche der Flüssigkeit längs
einer Linie von 1 mm eine Kraft gleich dem Gewichte eines Milligramms
bewirkt. Nach dem obigen kann man nun auch:
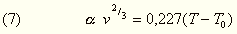
schreiben, wo T0 jene Temperatur bezeichnet,
bei welcher 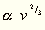 gleich
Null ist. Nach meinen Untersuchungen an Aether, Alkohol,
Kohlensäure u. a. scheint diese Temperatur mit der kritischen
zusammenzufallen oder wenigstens nicht weit davon entfernt zu sein.
gleich
Null ist. Nach meinen Untersuchungen an Aether, Alkohol,
Kohlensäure u. a. scheint diese Temperatur mit der kritischen
zusammenzufallen oder wenigstens nicht weit davon entfernt zu sein.
Zur experimentellen Bestätigung obiger Sätze stand mir ein sehr reiches Material, und zwar die Resultate von Beobachtungen an 160 verschiedenen, teils organischen, teils anorganischen Flüssigkeiten, zur Verfügung. Ich selbst bestimmte den Wert der Oberflächenspannung für eine Reihe von Flüssigkeiten, namentlich auch für einige kondensierte Gase; außerdem benutzte ich dazu die von R. Schiff in seinen beiden auf die Kapillaritätskonstanten bezüglichen Abhandlungen angegebenen Resultate. Die Vergleichung dieser letzteren mit meinen eigenen zeigte nur geringe Abweichungen.
Die erste Frage war, ob die Beobachtungen für Temperaturen, bei welchen die Gleichung (2) besteht, auch die Richtigkeit der Gleichungen (3), (4), (5) und (6) bestätigen. Mit Ausnahme einiger Körper, wie des Wassers, der Alkohole und der Fettsäuren, ergab sich eine befriedigende Übereinstimmung; die Abweichungen betragen höchstens fünf Prozente bei Berechnung der Oberflächenspannung aus meinen eigenen Beobachtungen, sowie auch aus jenen, die in der ersten Abhandlung von Schiff enthalten sind. Die in der zweiten Abhandlung desselben Verfassers befindlichen Werte geben etwas größere Abweichungen, wie dies auch leicht erklärlich ist, da darin die Werte der Kapillaritätskonstanten für die Siedetemperaturen aus empirischen Formeln durch Extrapolation berechnet wurden.
Das Hauptresultat meiner theoretischen Betrachtungen bestätigte
sich ebenfalls. Ich bestimmte den Wert des
Quotienten 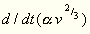 und fand diesen beispielsweise:
und fand diesen beispielsweise:
| Aethyläther | ...... | 6 | 62 | ... | 0,228 | ||||
| « | ...... | 62 | 120 | ... | 0,226 | ||||
| « | ...... | 120 | 190 | ... | 0,221 | ||||
| Aethylenbromid | ...... | 20 | 99 | ... | 0,227 | ||||
| « | ...... | 99 | 213 | ... | 0,232 | ||||
| Chloroform | ...... | 20 | 60 | ... | 0,230 | ||||
| Quecksilbermethyl | ...... | 20 | 99 | ... | 0,228 | ||||
| Kohlenstoffoxydchlorid | ...... | 3 | 63 | ... | 0,231 | ||||
| Kohlendioxyd | ...... | 3 | 31 | ... | 0,228 | ||||
| Schwefelkohlenstoff | ...... | 22 | 78 | ... | 0,237 | ||||
| Schwefelsäure | ...... | 2 | 60 | ... | 0,230 |
Werte, welche von diesen um nicht mehr als 0,02 abweichen, ergeben sich auch aus den von Schiff gewonnenen Beobachtungsresultaten.
Die oben angeführten Körper, nämlich das Wasser, die Alkohole und die Fettsäuren, bilden auch hier die Ausnahmen. Diese unterwarf ich einer genaueren Prüfung; den theoretischen Erörterungen gemäß können dieselben durch die Annahme erklärt werden, daß die betreffenden Körper im untersuchten Temperaturintervalle nicht einfach zusammengesetzt seien, daß also ihre Moleküle im flüssigen Zustande nicht die gleiche Masse wie im Dampfzustande haben. Es ist dies entweder auf die Weise möglich, daß die Flüssigkeit aus solchen gleichen Molekülen besteht, welche gleiche Vielfache der dampfbildenden Moleküle sind, oder aber daß die Flüssigkeit aus einem Gemenge solcher verschiedener Moleküle besteht, welche verschiedene Vielfache der dampfbildenden sind.
Ist aber bei einer Flüssigkeit in irgend einem Temporaturintervalle das erstere der Fall, so muß voraussichtlich beim Übergang zu anderen Temperaturen der zweite Fall eintreten. Jedenfalls muß dann bei der Erwärmung bis zur kritischen Temperatur eine Zersetzung der zusammengesetzten Moleküle der Flüssigkeit in solche des Dampfes stattfinden, da ja bei dieser Temperatur beide gleich werden.
Bei dieser Art physikalischer Zersetzung, welche von der chemischen Dissoziation wohl zu unterscheiden ist, bleibt es noch immer möglich, daß die zusammengesetzten Moleküle einer Flüssigkeit auch innerhalb größerer Temperaturintervalle unverändert bleiben, oder daß ihre Zersetzung plötzlich, vielleicht bei der kritischen Temperatur selbst, vor sich geht.
Ich untersuchte nun das Verhalten des Aethylalkohols, und zwar
bis zu seiner kritischen Temperatur, und fand als Wert des Quotienten
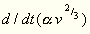 :
:
| 21 | 78 | ° C | ...0,104 | | | 138 | 168 | ° C | ...0,183 | ||||
| 78 | 108 | ...0,136 | | | 168 | 199 | ...0,202 | ||||||
| 108 | 138 | ...0,159 | | | 199 | 236 | ...0,226 |
Diese Zahlen scheinen dafür zu sprechen, daß die Moleküle dieser Flüssigkeit bei niederen Temperaturen zusammengesetzt sind und bei der Erwärmung eine stetig vor sich gehende Zersetzung erleiden, welche bei der Temperatur von 200° C beendet ist, da von dieser Temperatur an der Quotient den normalen Wert annimmt, entsprechend dem aus der Dampfdichte sich ergebenden Molekulargewichte.
Für Wasser ergeben sich mit Zugrundelegung der Formel H2O
Werte, welche auffallend klein sind; versuchsweise berechnete
ich daher den Wert des Quotienten mit Hilfe der Annahme doppelter
Moleküle, und es ergaben sich für denselben folgende
Werte:
| 3 | 40 | ° C | ...0,159 | | | 100 | 150 | ° C | ...0,228 | ||||
| 40 | 100 | ...0,180 | | | 150 | 210 | ...0,227 |
Dem entsprechend wären die Moleküle des flüssigen Wassers zwischen 100° und 210° C gleich den doppelten Molekülen des Dampfes, bei niederen Temperaturen aber noch größer. Für Temperaturen über 210° C konnte ich keine Beobachtungen mehr anstellen, da bei diesen die das Wasser enthaltenden Glasgefäße angegriffen wurden.
Aus der Reihe der Fettsäuren untersuchte ich besonders die
Essigäure und erhielt mit Zugrundelegung der Formel C2H4O2
die Werte:
| 21 | 107 | ° C | ...0,132 | |||
| 107 | 160 | ...0,132 | ||||
| 160 | 230 | ...0,138 |
Benutzen wir aber die Formel 2C2H4O2, so wird der Wert des Quotienten 0,211; es scheint demnach, daß die Moleküle der Essigsäure dieser zweiten Formel entsprechen, was wegen der anomalen Dampfdichte derselben auch wahrscheinlich ist.
Schließlich will ich noch erwähnen, daß ich auch am Quecksilber Messungen vorgenommen habe; ich erhielt für dasselbe zwischen 0° und 300° C den Wert 0,18. Dazu ist aber zu bemerken, daß sich dabei das Quecksilber in einem Temperaturintervalle befand, welches außerhalb jener Grenzen liegt, innerhalb deren die Gültigkeit meines Satzes ausgesprochen wurde.
Auch Gemische von Aether und Schwefelkohlenstoff unterwarf ich der Untersuchung und fand die oben abgeleiteten Sätze auch durch diese bestätigt, wobei als Molekularvolumen der Mittelwert v1+ kv2 : 1+k der beiden Molekularvolumina v1 und v2 genommen wurde bei dem Mischungsverhältnisse k.